今日學習重點

現在你已經了解一些有關於Seq2Seq的知識，接下來我們要告訴你的是注意力機制(Attention)的特點，以及它如何解決僅通過上下文向量傳遞資訊的問題。

1. 學習注意力機制(Attention)的功能
2. 理解Encoder與Decoder之間的訊息拼接方式
3. 理解Decoder怎麼通過注意力機制生成文字

注意力機制(Attention)

注意力機制(Attention)模擬了人類的專注力特性，讓電腦在處理信息時有選擇地專注於某些部分，而忽略其他不重要的訊息，而注意力機制在Seq2Seq這種Encoder-Decoder模型架構裡的核心功能即是將各層Encoder的隱狀態h(t)選擇出最佳解，使其傳遞給Decoder進行比對後進行生成的動作，藉此讓Decoder能更深入地理解這些信息。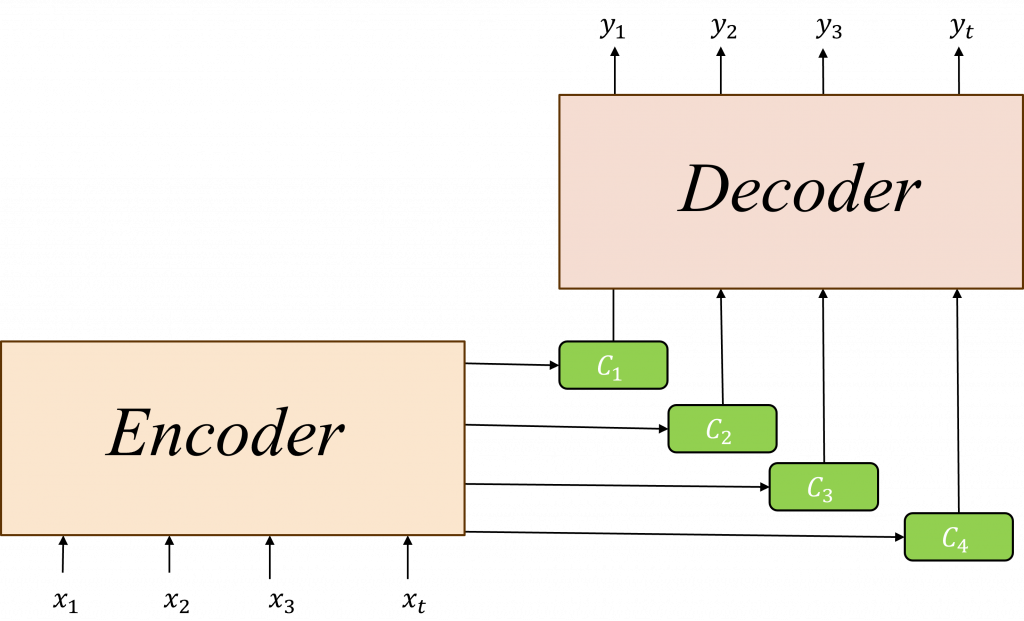

而在注意力機制，需要先計算注意力分數（Attention Scores）、注意力權重（Attention Weights）已產生更好的上下文向量（Context Vector），以下我將會用公式對此進行詳細的解析動作。

注意力分數（Attention Scores）

在採用注意力機制的Encoder架構中，我們不會僅用一個隱狀態讓Decoder進行生成，而是讓Decoder需要在每次生成文字時，都找出最有可能的Encoder的隱狀態，所以我們必須使其先行計算出注意力分數，使其能找到最有可能的結果，其計算公式如下: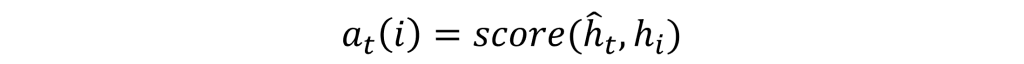

在上述公式中，Encoder隱狀態h(i)將與每一個Decoder的隱狀態hd(t)進行對比與分析，其中score()有非常多的變化與形式，它可以透過內積、點積和拼接等方法進行計算，而大多數會用運以上公式來進行計算注意力分數的動作。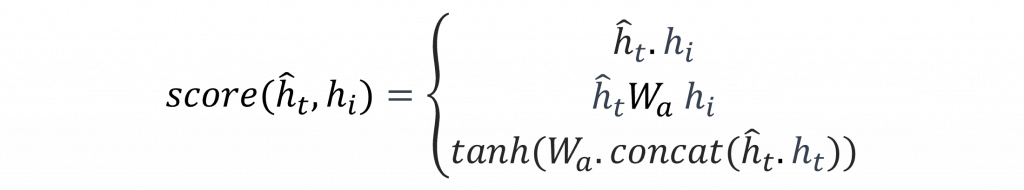

不過要如何選擇這些方式就需要進行實驗比對才能判別對當前任務的效用，而這些公式的含意接代表著將Encoder與Deceder兩者的隱狀態訊息完整的整合在一起。

注意力權重（Attention Weights）

在以上的公式中，我們只是計算出所有的排列組合分數，然而這個分數通常表示的是一個數值而不是機率，因此當我們計算出注意力分數後，還需要透過softmax函數來轉換為注意力權重，這樣能夠讓我們找出這些組合中機率最高的結果。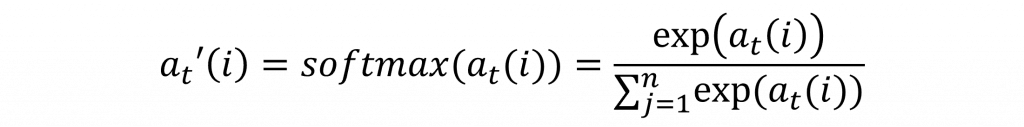

透過以上的公式透過不斷的迭代運算，使其能夠計算出h(i)與hd(t)之間的機率，這時我們就可以透過這個機率與Encoder中的h(i)進行運算，藉此找出輸入給Decoder的上下文向量。

上下文向量（Context Vector）

因此在計算上下文向量的過程中，我們需要將h(i)不斷的與所有的注意力權重at'(i)進行運算，其計算公式如下: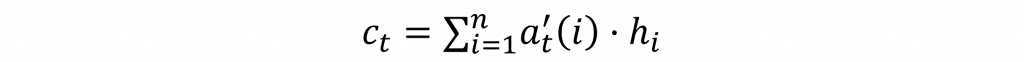

通過以上的計算流程，我們讓Encoder中的的隱狀態動態地調整注意力權重，使Decoder可以產生更準確的序列輸出，在模型訓練的過程中，將會訓練出Encoder-Eeocder的隱藏狀態與權重組合，進而提供了更多特徵輸入序列的資訊。

後話

在昨日與今天我們學習了Seq2Seq的完整架構以及其改善方法，你或許已經注意到與先前相比，這兩天的學習內容相對較少，原因在於我們才剛剛掌握了時間序列模型的基本理論，因此在學習Seq2Seq時，你可能會發現自己常常需要回頭檢視先前學過的公式內容。加上Seq2Seq與Attention的公式特別多，因此在撰寫程式時建構的複雜程度也相當的高，因此我決定用兩天的時間來詳細講解這個部分，並規劃在明天教你一個如何建立完整的機器翻譯模型。

那麼我們明天再見！

內容中的程式碼都能從我的GitHub上取得:
https://github.com/AUSTIN2526/iThome2023-learn-NLP-in-30-days